Packing bits into JavaScript strings

JavaScript code samples in this article are licensed under CC BY.

(This is the second article in the series for Golf Horse: Wordle.)

For our JavaScript code golf challenge, we’d like to be able to pack as many bits as we can into our source code, which must be UTF-8. In our previous article, we determined that UTF-8 can theoretically store 7.1756 bits per byte. However, that bound is not achievable; we have additional considerations:

JavaScript syntax limits the Unicode characters we can put in our source code.
We need to consider code size tradeoffs. A decoder that reaches the theoretical bound might not be helpful if it results in large code size. We’re optimizing for the minimum of (code size) + (compressed data size).

We’ll take a deeper look at each of these constraints, then we’ll take a look at the decoder I decided on for my entry.

JavaScript string constraints

A quick summary of the rules for JavaScript (ES6) string syntax:

Quoted strings, using either single quotes ' or double quotes ", restrict the following four characters:
- Backslash \, because it’s used for escape sequences
- Carriage return U+000D, because newlines are not supported within quoted strings
- Line feed U+000A, same reason as carriage return
- The same type of quote that began the string literal, because it marks the end of the string literal
Template literals also restrict four characters, but different:
- Backslash, because it’s used for escape sequences
- Carriage return, because it’s parsed the same as line feed
- Dollar sign $, because it’s used for interpolation
  (Edit 21Dec23: Dollar sign, if not followed by an open bracket, is allowed. This article doesn’t consider this possibility, but it would be quite helpful to allow it. Hopefully I will have a new article with improved techniques in the future—stay tuned!)
- Backtick `, because that’s used to end the template literal
String.raw is similar to template literals, but escape sequences aren’t parsed. So, the backslash character is available, and only three characters are restricted.

In summary, quoted strings and template literals allow us to include all but four Unicode characters. String.raw allows us to include all but three Unicode characters.

That makes String.raw look like the best option, but it’s not so clear! String.raw adds 10 characters to our source code compared to the other options, for example:

"hello, world!";            //quoted string
`hello, world!`;            //template literal
String.raw`hello, world!`;  //raw string, +10 bytes

We’ll need to do some testing to figure out if the 10 extra bytes of source code is worth the one extra Unicode character we can use. We’ll defer the calculation for after we have an implementation developed.

Theoretical capacity

In the previous article, we found the theoretical capacity of UTF-8 by solving

$b^4 = 128b^3 + 1920b^2 + 61440b + 1048576$

where 128 is the number of 1-byte Unicode characters, 1920 is the number of 2-byte characters, etc. This has the solution $b=144.57$ giving a data capacity of $\log_2 144.57 = 7.1756$ bits per byte. Let’s repeat the calculation for JavaScript strings:

For quoted strings and template literals, we lose four 1-byte characters. So our new equation is
$b^4 = 124b^3 + 1920b^2 + 61440b + 1048576$
This has the positive root 141.071, giving a theoretical capacity of 7.1403 bits per byte.
For raw strings, we lose three 1-byte characters. So our new equation is
$b^4 = 125b^3 + 1920b^2 + 61440b + 1048576$
This has the positive root 141.943, giving a theoretical capacity of 7.1492 bits per byte.

In summary,

                    Bits/Byte
Quoted strings      7.1403
Raw strings         7.1492
Unrestricted UTF-8  7.1756

The next step is to dive into decoders that can achieve these theoretical bounds!

Entropy coding

We’ll briefly go through one approach to developing a decoder for compressed data. To avoid getting too far afield, I’m going to omit most of the underlying mathematical theory. If you’re interested, have a look into entropy coding and arithmetic coding.

The goal of our decoder is to take a source of compressed data and convert it to a sequence of bits. Furthermore, for each bit to be decoded, we’d like to assign a probability that it’s 0. Those probabilities, if accurate, will help us compress the bits better. (We’ll discuss the probability modeling in a future article, for now, just assume we have a source for them.)

A method to achieve (asymptotically) optimal encoding is arithmetic coding. The idea is to start with the interval [0,1) and repeatedly partition it according to the probabilities of the bits. Let $p_i$ be the probability that bit i is 0. We’ll start by partitioning [0,1) into $[0,p_0)$ and $[p_0,1)$. If the first bit we’re compressing is 0, then we’ll take the interval $[0,p_0)$, else we take the interval $[p_0,1)$. Then we repeat for the second bit: we’ll split the new interval proportionally to $(p_1):(1-p_1)$ and choose the first interval if the second bit is 0, otherwise the second interval if the bit is 1. After doing this for all our bits, we’ll have a very small interval remaining.

Here’s a visual example if the probabilities are 0.4, 0.75, 0.2 and the bits are 0, 1, 1:

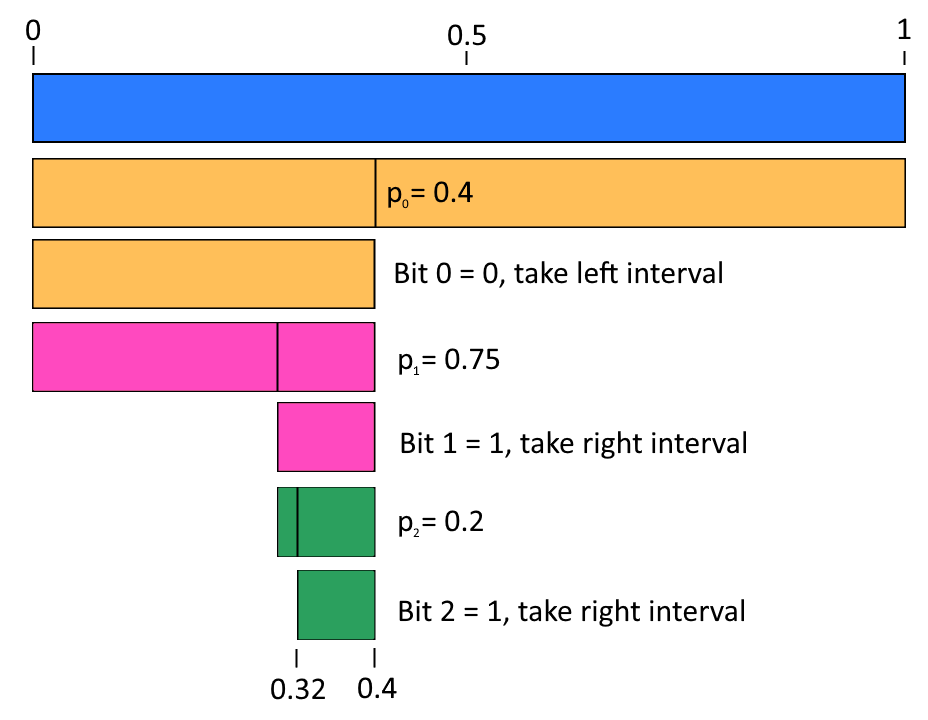
Next, we can choose a real number r inside the final interval. The trick to this encoding/decoding technique is that the $p_i$ combined with r is enough to identify all our bits!

We’ll represent r by its expansion in base b, where b is some number we’ll choose later. That is,

$\displaystyle r = \sum_{i=0}^\infty a_ib^i$

where $a_i$ is the base-b expansion. Our compressed data is then simply the $a_i$. (Note that although the sum is infinite, we don’t actually need infinite terms in practice, because we can always choose some r with a finite representation. Mathematically speaking, the numbers with finite base-b expansion are dense.)

In summary,

Start with the interval [0,1).
Recursively split the interval proportionally into $(p_i):(1-p_i)$, choose the first interval if the ith bit is 0 and the second if the bit is 1. Do this for all the bits and $p_i$.
Choose a real number r in the final interval with finite base-b representation.
This base-b representation of r is the compressed data.

Next, we’ll look at implementation! There are two parts: first we’ll look at the decoder, which takes the $a_i$ and $p_i$ and outputs our bits. Second, we’ll take a look at efficient options for converting a JavaScript string to the $a_i$.

Decoder implementation

Our decoder is the reverse of encoding as we described above. The main difficulty is dealing with precision issues: the endpoints of the interval become very long decimals. However, for implementation, we don’t want to actually work with arbitrary precision real numbers. Instead, we’ll work with limited precision, where we ignore early digits that become irrelevant, and pull in more digits as we need them. Here’s the code:

base = 138;
compressed_data = [42, 31, 41, 120, 99]; //the a_i
compressed_data_index = 0;

r_high = 1; //the current interval is [0, r_high)
r = 0; //where we are in the current interval

function decode_next_bit(probability)
{
  //Grab more data if our interval is too small
  while(r_high < 1000)
  {
    r_high *= base;
    r *= base;
    r += compressed_data[compressed_data_index++];
  }

  //Check if next bit is 0 or 1 based on the probability
  threshold = Math.floor(probability * r_high);
  if(r < threshold)
  {
    //Take the left interval and return 0
    r_high = threshold;
    return 0;
  }
  else
  {
    //Take the right interval and return 1
    r -= threshold;
    r_high -= threshold;
    return 1;
  }
}

(I should mention that there’s a potential issue with this code if the probability is close to 0 or 1. Under some circumstances, r_high can become 0, and the decoder will be stuck. In a production-worthy implementation, you may want to bound the threshold by [1, r_high - 1].)

I was happy about this decoder, as the implementation is quite simple and it golfs down to very small code size. (I can’t easily show the golfed code here, because in my actual submission, the decoder wasn’t a single function. It was scattered across the code. My final article will have the submission’s code.) However, there is a major caveat: the encoder is complicated! The way the decoder shifts in new data is hard to reverse for encoding. (Real-world arithmetic decoders work slightly differently to ensure the encoding process is easy.) The encoder I wrote used bisection to find the $a_i$, which is both difficult and inefficient. However, the encoder isn’t part of the final program, so I was optimizing only for the decoder size.

Strings to numbers

The decode_next_bit algorithm above assumes the compressed data is a sequence of numbers, not Unicode characters. However, we want to store our compressed data as a Unicode string. So, let’s write some code to convert a string to a sequence of numbers, and let’s analyze how it affects our data compression ratio.

A simple idea is to convert a character to its Unicode code point value. Recall that we have 3 or 4 characters we can’t include in our string (depending which string syntax we use). We should skip over these code points, which we can do as follows:

compressed_string = `38yV F02`;
compressed_data = [];
for(char of compressed_string)
{
  x = char.codePointAt(0);
  if(x > 96) x--; //skip backtick
  if(x > 92) x--; //skip backslash
  if(x > 36) x--; //skip dollar sign
  if(x > 13) x--; //skip newline
  compressed_data.push(x);
}

//compressed_data will be [49, 54, 117, 84, 31, 68, 46, 48]

While this works, it’s not efficient. We’re generating exactly one numerical value per character, but Unicode characters can occupy 1, 2, 3, or 4 bytes. That makes 2-, 3-, and 4-byte characters wasteful compared to 1-byte characters.

We face an interesting optimization problem: how to assign multi-byte Unicode characters to multiple numerical values, such that we can maximize the information we can encode. Let’s do one example in detail.

Base-137 decoder example

We choose a base of 137, so our numerical values should cover the range [0, 136].
Assuming we use template literals for our source data, we have 124 1-byte characters we can use, so let’s assign them to the values 0 through 123.
We’ll assign 2-byte characters to pairs of numbers as follows:
- The first 137 2-byte characters represent the pairs (124, 0) through (124, 136).
- The next 137 2-byte characters represent the pairs (125, 0) through (125, 136).
- Continue until we’ve covered up to (136, 136). That’s a total of 13 * 137 = 1781 2-byte characters. We have 1920 available, so we’re covered.

function string_to_numbers_137(compressed_string)
{
  ret = [];
  for(char of compressed_string)
  {
    x = char.codePointAt(0);
    if(x > 96) x--; //skip backtick
    if(x > 92) x--; //skip backslash
    if(x > 36) x--; //skip dollar sign
    if(x > 13) x--; //skip newline
    if(x < 124)
    {
      //1-byte character
      ret.push(x);
    }
    else
    {
      //2-byte character
      x -= 124;
      ret.push(Math.floor(124 + x / 137));
      ret.push(x % 137);
    }
  }
  return ret;
}

string_to_numbers_137(`hi\x7F\x80\x81`)
/*We use escaped Unicode characters for legibility; in
the actual submission they appear literally.
Outputs [100, 101, 123, 124, 0, 124, 1] because
h => 100
i => 101
\x7F => 123
\x80 => 124, 0 (2-byte Unicode character)
\x81 => 124, 1 (2-byte Unicode character)
*/

To compute the information capacity, recall that it’s $\log_2$ of the number of possibilities. Because we chose base 137, each number in the output adds $\log_2 137$ bits of information. In this scheme, 1-byte characters give us one number, and 2-byte characters give us two numbers, so we get one number per byte. Our information capacity is $\log_2 137 = 7.098$ bits per byte.

Compared to the optimal 7.1403 bits per byte, we’re doing okay but not great. There’s room for improvement; let’s look at more possibilities.

Lots more decoder options

In addition to the base-137 example above, here are some other options I considered:

Base 138 with quoted strings/template literals: Assign the 124 available 1-byte characters to values 0 through 123. We then need to cover the pairs (124, X) through (137, X), of which there are 14 * 138 = 1932. Assign all 1920 2-byte characters to these pairs, and assign 12 3-byte characters to the remaining pairs. Capacity is 7.104 bits per byte.
Base 138 with raw strings: Assign the 125 available 1-byte characters to values 0 through 124. Assign 2-byte characters to the pairs (125, X) through (137, X), of which there are 13 * 138 = 1794. Capacity is 7.109 bits per byte.
Base 140 with quoted strings/template literals: Assign the 124 available 1-byte characters to values 0 through 123. Assign the 1920 2-byte characters to the pairs (124, 0) through (137, 99). Assign 44800 3-byte characters to the triplets (137, 100, 0) through (139, 139, 139). Capacity is 7.1293 bits per byte.
Base 141 with quoted strings/template literals: Assign 124 1-byte characters to single values, 1920 2-byte characters to pairs, 61440 3-byte characters to triplets, and 820197 4-byte characters to quadruplets. Capacity is 7.1396 bits per byte.
Base 142 with raw strings: Assign 125 1-byte characters to single values, 1920 2-byte characters to pairs, 61440 3-byte characters to triplets, 1334 4-byte characters to triplets, and 1047108 4-byte characters to quadruplets. Capacity is 7.1468 bits per byte.

To summarize,

Using quoted strings or template literals
-----------------------------------------
                  Bits/byte
Base 137          7.0980
Base 138          7.1045
Base 140          7.1293
Base 141          7.1396
Theoretical max   7.1403

Using raw strings
-----------------
                  Bits/byte
Base 138          7.1085
Base 142          7.1468
Theoretical max   7.1492

After coding a few of these up, the tradeoff for code size versus compressed data size was clear. For the size of the data I needed to encode—about 74k bits—base 138 with quoted strings was the winner.

For larger data sets, the code size tradeoff will be different, and the more complex algorithms for larger bases would be useful.

The base 138 decoder is a quick modification to the base 137 decoder above:

function string_to_numbers_138(compressed_string)
{
  ret = [];
  for(char of compressed_string)
  {
    x = char.codePointAt(0);
    if(x > 96) x--; //skip backtick
    if(x > 92) x--; //skip backslash
    if(x > 36) x--; //skip dollar sign
    if(x > 13) x--; //skip newline
    if(x < 124)
    {
      //1-byte character
      ret.push(x);
    }
    else
    {
      //2-byte character
      x -= 124;
      ret.push(Math.floor(124 + x / 138));
      ret.push(x % 138);
    }
  }
  return ret;
}

string_to_numbers_138(`hi\x7F\x80\x81`)
//Outputs [100, 101, 123, 124, 0, 124, 1]

Golfing it down,

b=138;l=124;e=[];for(x of`hi\x7F\x80\x81`){a=x.charCodeAt(0);for(z of`\x0C#[_`)a-=x>z;e.push(...a<l?[a]:[(a-=l)/b+l|0,a%b])};
//Output is in e

My submission’s decoder was even smaller than this, as I used a different mapping from characters to values, allowing me to remove usages of 124. My last article will contain the actual code for my submission, so all tricks will be revealed!

Conclusion

To summarize our overall strategy,

Store compressed data as a template literal in the source code.
Convert the compressed data to an array of numbers using the base-138 conversion routine string_to_numbers_138.
Convert the array of numbers to bits using the arithmetic decoder decode_next_bit.

With this strategy, we can store 7.104 bits per byte of source code with a fairly small decoder. With a larger code size, we could use a more complex decoder that achieves even more bits per byte, but that tradeoff isn’t profitable for this code golf challenge.

Packing bits into JavaScript strings

Packing bits into JavaScript strings

JavaScript string constraints

Theoretical capacity

Entropy coding

Decoder implementation

Strings to numbers

Base-137 decoder example

Lots more decoder options

Conclusion

Leave a Reply Cancel reply